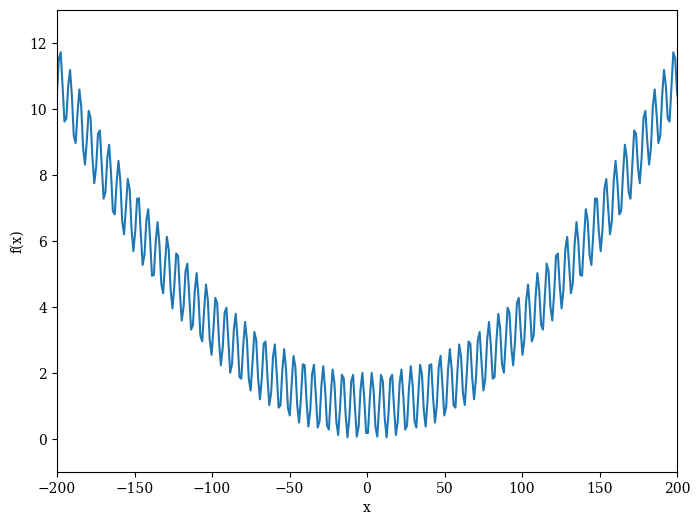
Griewank¶
The Griewank function has many widespread local minima, which are regularly distributed. The complexity is shown in the zoomed-in plots.
Definition
\begin{align} \begin{split} f(x) & = & \; \sum_{n=1}^n \; \frac{x_i^2}{4000} - \prod_{n=1}^n \cos \Bigg( \frac{x_i}{\sqrt{i}} \Bigg) + 1 \\[4mm] &&-600 \leq x_i \leq 600 \quad i=1 \ldots,n \\[4mm] \end{split} \end{align}
Optimum
\[f(x^*) = 0 \; \text{at} \; x^* = (0,\ldots,0)\]
Contour
[1]:
from pymoo.problems import get_problem
from pymoo.visualization.fitness_landscape import FitnessLandscape
problem = get_problem("griewank", n_var=1)
plot = FitnessLandscape(problem, _type="surface", n_samples=1000)
plot.do()
plot.apply(lambda ax: ax.set_xlim(-200, 200))
plot.apply(lambda ax: ax.set_ylim(-1, 13))
plot.show()
[1]:
<pymoo.visualization.fitness_landscape.FitnessLandscape at 0x11701bc50>