C-TAEA¶

This algorithm is implemented based on [2] and the authors’ implementation. The algorithm is based on Reference Directions which need to be provided when initializing the algorithm object.

C-TAEA follows a two archive approach to balance convergence (Convergence Archive CA) and diversity (Diversity Archive DA).

[1]:

from pymoo.algorithms.moo.ctaea import CTAEA
from pymoo.problems import get_problem
from pymoo.util.ref_dirs import get_reference_directions
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter

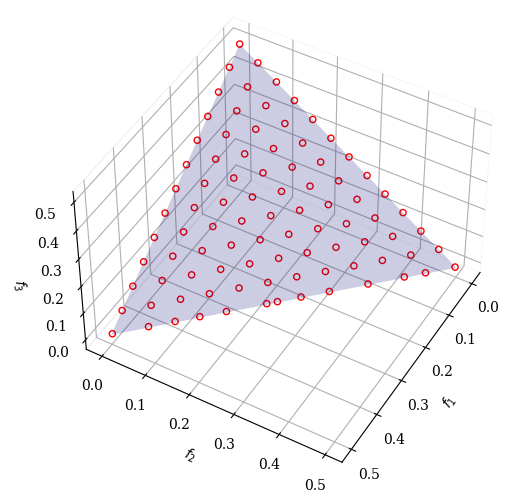
problem = get_problem("c1dtlz1", None, 3, k=5)

ref_dirs = get_reference_directions("das-dennis", 3, n_partitions=12)

# create the algorithm object
algorithm = CTAEA(ref_dirs=ref_dirs)

# execute the optimization
res = minimize(problem,
               algorithm,
               ('n_gen', 600),
               seed=1,
               verbose=False
               )

sc = Scatter(legend=False, angle=(45, 30))
sc.add(problem.pareto_front(ref_dirs), plot_type='surface', alpha=0.2, label="PF", color="blue")
sc.add(res.F, facecolor="none", edgecolor="red")
sc.show()

[1]:

<pymoo.visualization.scatter.Scatter at 0x12d346ab0>

../../_images/algorithms_moo_ctaea_2_1.png

[2]:

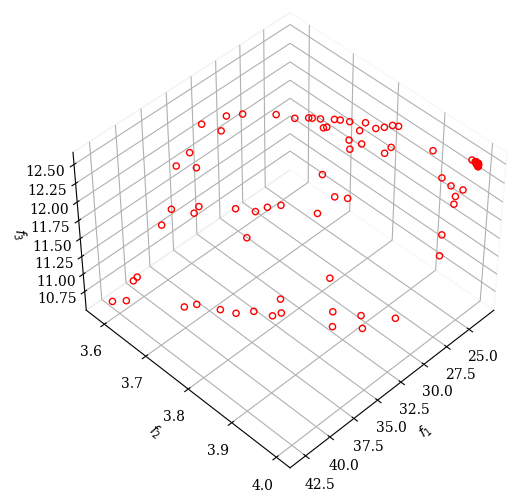
problem = get_problem("carside")
ref_dirs = get_reference_directions("das-dennis", problem.n_obj, n_points=91)
algorithm = CTAEA(ref_dirs=ref_dirs)

res = minimize(problem,
               algorithm,
               ('n_gen', 600),
               seed=1
               )

Scatter().add(res.F, facecolor="none", edgecolor="red").show()

[2]:

<pymoo.visualization.scatter.Scatter at 0x12d5be3c0>

../../_images/algorithms_moo_ctaea_3_1.png

API¶

class pymoo.algorithms.moo.ctaea.CTAEA(self, ref_dirs, sampling=FloatRandomSampling(), selection=RestrictedMating(func_comp=comp_by_cv_dom_then_random), crossover=SBX(n_offsprings=1, eta=30, prob=1.0), mutation=PM(prob_var=None, eta=20), eliminate_duplicates=True, output=MultiObjectiveOutput(), **kwargs)

CTAEA

Parameters

ref_dirsnumpy.array: The reference direction that should be used during the optimization. Each row represents a reference line and each column a variable.
samplingSampling, Population, numpy.array: The sampling process defines the initial set of solutions which are the starting point of the optimization algorithm. Here, you have three different options by passing

(i) A Sampling implementation which is an implementation of a random sampling method.

(ii) A Population object containing the variables to be evaluated initially OR already evaluated solutions (F needs to be set in this case).

(iii) Pass a two dimensional numpy.array with (n_individuals, n_var) which contains the variable space values for each individual.
selectionSelection: This object defines the mating selection to be used. In an evolutionary algorithm each generation parents need to be selected to produce new offsprings using different recombination and mutation operators. Different strategies for selecting parents are possible e.g. selecting them just randomly, only in the neighborhood, using a tournament selection to introduce some selection pressure, …
crossoverCrossover: The crossover has the purpose of create offsprings during the evolution. After the mating selection the parents are passed to the crossover operator which will dependent on the implementation create a different number of offsprings.
mutationMutation: Some genetic algorithms rely only on the mutation operation. However, it has shown that increases the performance to perform a mutation after creating the offsprings through crossover as well. Usually the mutation operator needs to be initialized with a probability to be executed. Having a high probability of mutation will most of the time increase the diversity in the population.
eliminate_duplicatesbool: The genetic algorithm implementation has a built in feature that eliminates duplicates after merging the parent and the offspring population. If there are duplicates with respect to the current population or in the offsprings itself they are removed and the mating process is repeated to fill up the offsprings until the desired number of unique offsprings is met.

Python implementation by cyrilpic based on the original C code.