BRKGA: Biased Random Key Genetic Algorithm¶

An excellent and very informative presentation about BRKGAs can be found here. BRKGAs are known to perform well-known on combinatorial problems.

5f2d713950574d62acb0b67d73a7bc59

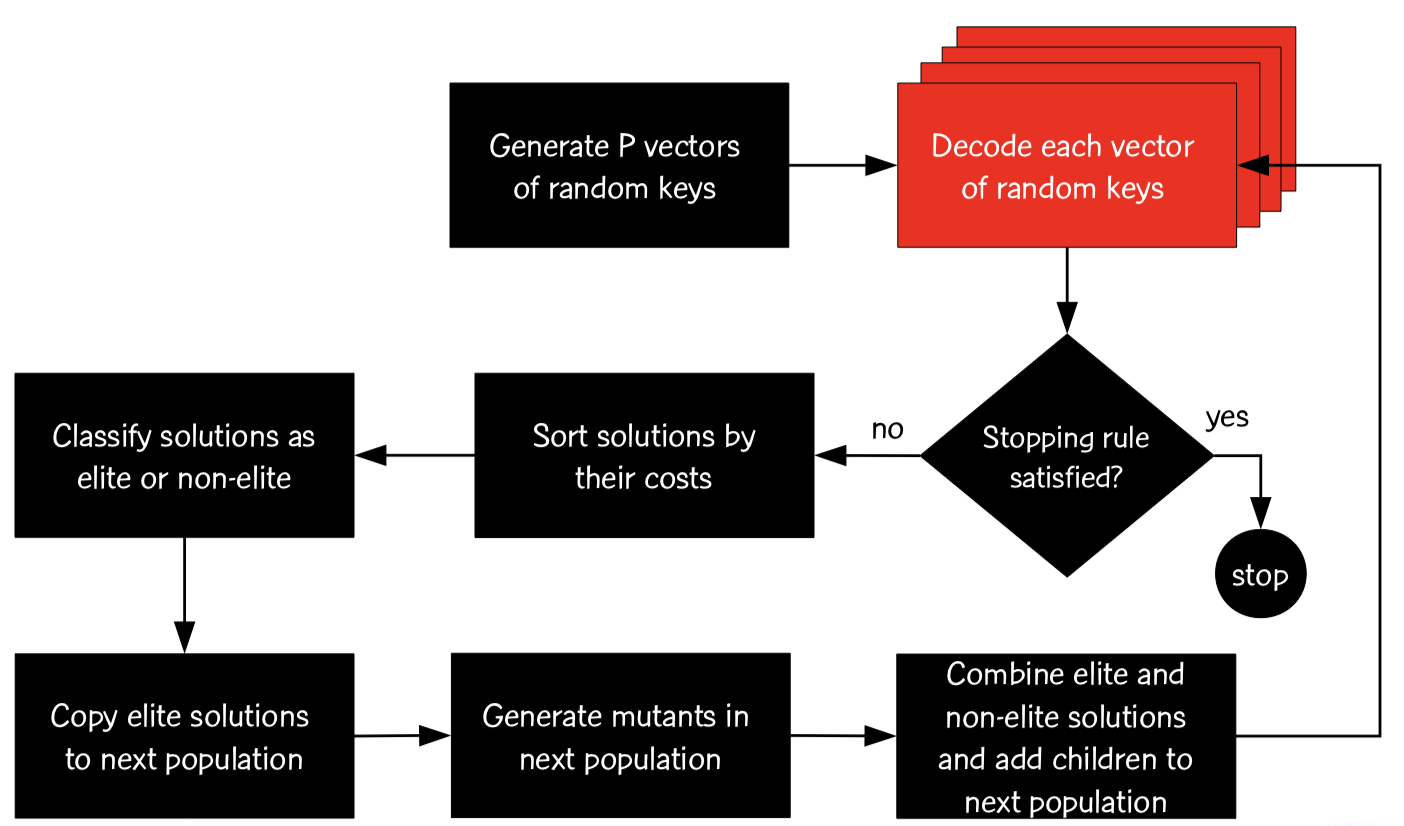
Instead of customizing evolutionary operators, decoding has to be defined. Therefore, evolution takes place solely on real-valued variables.

Let us define a permutation problem which derives an order by sorting real-valued variables:

[1]:

import numpy as np

from pymoo.core.problem import ElementwiseProblem


class MyProblem(ElementwiseProblem):

    def __init__(self, my_list):
        self.correct = np.argsort(my_list)
        super().__init__(n_var=len(my_list), n_obj=1, n_ieq_constr=0, xl=0, xu=1)

    def _evaluate(self, x, out, *args, **kwargs):
        pheno = np.argsort(x)
        out["F"] = - float((self.correct == pheno).sum())
        out["pheno"] = pheno
        out["hash"] = hash(str(pheno))

Since duplicate eliminates is an essential aspect for evolutionary algorithms, we have to make sure all duplicates with respect to the permutation (and not to the real values) are filtered out.

[2]:

from pymoo.core.duplicate import ElementwiseDuplicateElimination

class MyElementwiseDuplicateElimination(ElementwiseDuplicateElimination):

    def is_equal(self, a, b):
        return a.get("hash") == b.get("hash")

Then, we define a problem that has to sort a list by their values.

[3]:

np.random.seed(2)
list_to_sort = np.random.random(20)
problem = MyProblem(list_to_sort)
print("Sorted by", np.argsort(list_to_sort))

Sorted by [ 1 19 12 14  6  9  8  5  4  3  0 17 13 11  2  7 10 15 18 16]

Finally, we use BRKGA to obtain the sorted list:

[4]:

from pymoo.algorithms.soo.nonconvex.brkga import BRKGA
from pymoo.optimize import minimize

algorithm = BRKGA(
    n_elites=200,
    n_offsprings=700,
    n_mutants=100,
    bias=0.7,
    eliminate_duplicates=MyElementwiseDuplicateElimination())

res = minimize(problem,
               algorithm,
               ("n_gen", 75),
               seed=1,
               verbose=False)

print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))
print("Solution", res.opt.get("pheno")[0])
print("Optimum ", np.argsort(list_to_sort))

Best solution found:
X = [0.43726815 0.03836057 0.64762066 0.41034453 0.36940481 0.33756292
 0.23897219 0.66828899 0.3159229  0.25393386 0.73439704 0.63393382
 0.11276644 0.63343317 0.13990858 0.91657459 0.99143067 0.58340631
 0.96917335 0.0441548 ]
F = [-20.]
Solution [ 1. 19. 12. 14.  6.  9.  8.  5.  4.  3.  0. 17. 13. 11.  2.  7. 10. 15.
 18. 16.]
Optimum  [ 1 19 12 14  6  9  8  5  4  3  0 17 13 11  2  7 10 15 18 16]

API¶

class pymoo.algorithms.soo.nonconvex.brkga.BRKGA(self, n_elites=200, n_offsprings=700, n_mutants=100, bias=0.7, sampling=FloatRandomSampling(), survival=None, output=SingleObjectiveOutput(), eliminate_duplicates=False, **kwargs)

Parameters

n_elitesint: Number of elite individuals
n_offspringsint: Number of offsprings to be generated through mating of an elite and a non-elite individual
n_mutantsint: Number of mutations to be introduced each generation
biasfloat: Bias of an offspring inheriting the allele of its elite parent
eliminate_duplicatesbool or class: The duplicate elimination is more important if a decoding is used. The duplicate check has to be performed on the decoded variable and not on the real values. Therefore, we recommend passing a DuplicateElimination object. If eliminate_duplicates is simply set to True, then duplicates are filtered out whenever the objective values are equal.