Mutation#
Polynomial Mutation (PM)#
Details about the mutation can be found in [41]. This mutation follows the same probability distribution as the simulated binary crossover.
[1]:
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.population import Population
from pymoo.core.problem import Problem
from pymoo.operators.mutation.pm import PolynomialMutation
def show(eta_mut):
problem = Problem(n_var=1, xl=0.0, xu=1.0)
X = np.full((5000, 1), 0.5)
pop = Population.new(X=X)
mutation = PolynomialMutation(prob=1.0, eta=eta_mut)
off = mutation(problem, pop)
Xp = off.get("X")
plt.hist(Xp, range=(0.0, 1.0), bins=200, density=True, color="red")
plt.show()
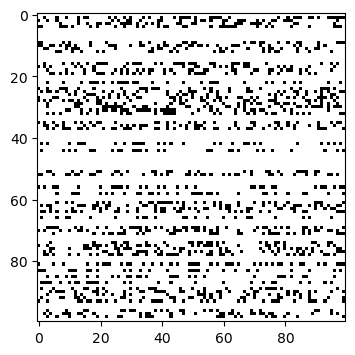
show(30)
[2]:
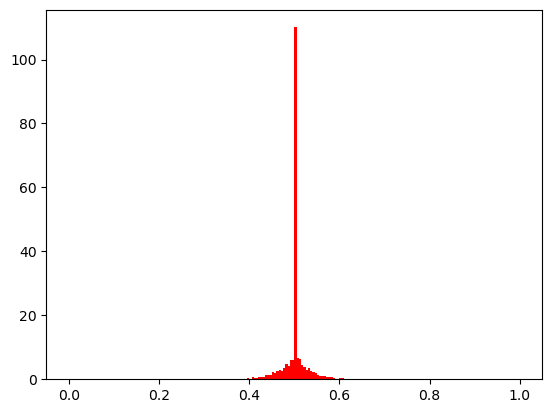
show(10)
Basically, the same can be applied to discrete variables as well:
[3]:
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.population import Population
from pymoo.core.problem import Problem
from pymoo.operators.mutation.pm import PolynomialMutation
from pymoo.operators.repair.rounding import RoundingRepair
def show(eta_mut):
problem = Problem(n_var=1, xl=-20, xu=20)
X = np.full((5000, 1), 0.0)
pop = Population.new(X=X)
mutation = PolynomialMutation(prob=1.0, eta=eta_mut, repair=RoundingRepair())
off = mutation(problem, pop)
Xp = off.get("X")
plt.hist(Xp, range=(-20, 20), bins=40, density=True, color="red")
plt.show()
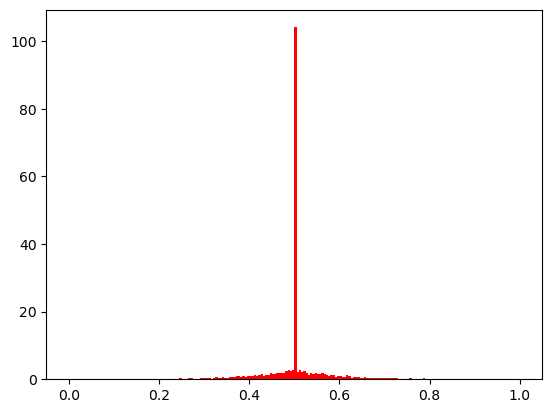
show(30)
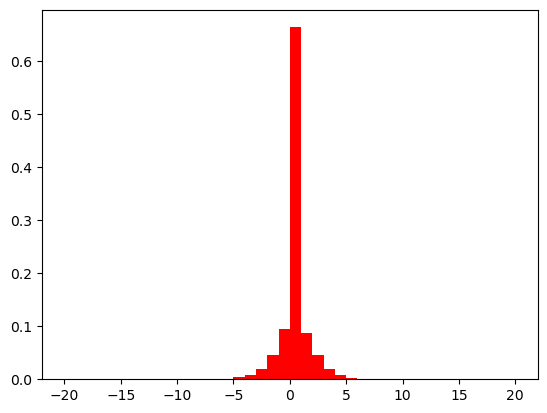
Bitflip Mutation (BM)#
The bitflip mutation randomly flips a bit.
[4]:
import matplotlib.pyplot as plt
import numpy as np
from pymoo.core.population import Population
from pymoo.core.problem import Problem
from pymoo.operators.mutation.bitflip import BitflipMutation
n_var, n_matings = 100, 50
problem = Problem(n_var=n_var, vtype=bool)
X = np.full((100, 100), False)
pop = Population.new(X=X)
mutation = BitflipMutation(prob=0.5, prob_var=0.3)
Xp = mutation(problem, pop).get("X")
plt.figure(figsize=(4, 4))
plt.imshow(X != Xp, cmap='Greys', interpolation='nearest')
plt.show()