SMS-EMOA: Multiobjective selection based on dominated hypervolume¶

The algorithm is implemented based on [12]. The hypervolume measure (or s-metric) is a frequently applied quality measure for comparing the results of evolutionary multiobjective optimization algorithms (EMOA).

200877273123421fb7060f1ea2f674fb

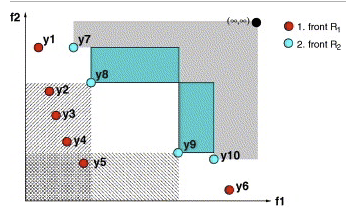
SMS-EMOA aims to maximize the dominated hypervolume within the optimization process. It features a selection operator based on the hypervolume measure combined with the concept of non-dominated sorting. As a result, the algorithm’s population evolves to a well-distributed set of solutions, focusing on interesting regions of the Pareto front.

Info

Note that the hypervolume metric becomes computationally very expensive for more than three objectives.

Example¶

[1]:

from pymoo.algorithms.moo.sms import SMSEMOA
from pymoo.optimize import minimize
from pymoo.problems import get_problem
from pymoo.visualization.scatter import Scatter

problem = get_problem("zdt1")

algorithm = SMSEMOA()

res = minimize(problem,
               algorithm,
               ('n_gen', 200),
               seed=1,
               verbose=False)

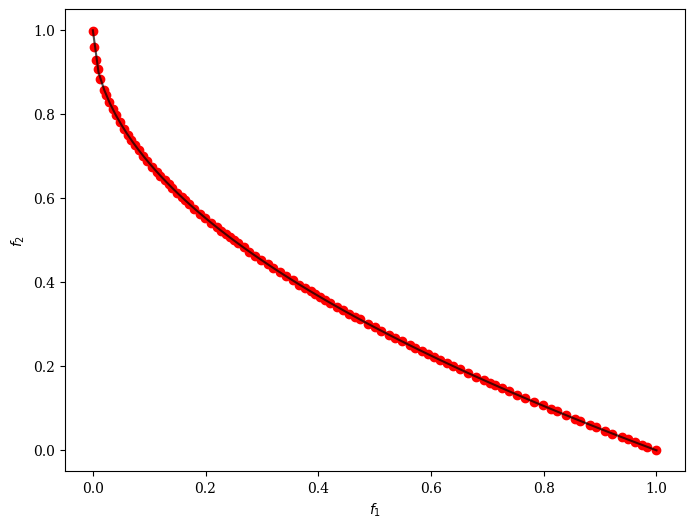
plot = Scatter()
plot.add(problem.pareto_front(), plot_type="line", color="black", alpha=0.7)
plot.add(res.F, color="red")
plot.show()

[1]:

<pymoo.visualization.scatter.Scatter at 0x120c23590>

../../_images/algorithms_moo_sms_7_1.png

API¶

class pymoo.algorithms.moo.sms.SMSEMOA(self, pop_size=100, sampling=FloatRandomSampling(), selection=TournamentSelection(func_comp=cv_and_dom_tournament), crossover=SBX(), mutation=PM(), survival=LeastHypervolumeContributionSurvival(), eliminate_duplicates=True, n_offsprings=None, normalize=True, output=MultiObjectiveOutput(), **kwargs)

Parameters

pop_sizeint: The population sized used by the algorithm.
samplingSampling, Population, numpy.array: The sampling process defines the initial set of solutions which are the starting point of the optimization algorithm. Here, you have three different options by passing

(i) A Sampling implementation which is an implementation of a random sampling method.

(ii) A Population object containing the variables to be evaluated initially OR already evaluated solutions (F needs to be set in this case).

(iii) Pass a two dimensional numpy.array with (n_individuals, n_var) which contains the variable space values for each individual.
selectionSelection: This object defines the mating selection to be used. In an evolutionary algorithm each generation parents need to be selected to produce new offsprings using different recombination and mutation operators. Different strategies for selecting parents are possible e.g. selecting them just randomly, only in the neighborhood, using a tournament selection to introduce some selection pressure, …
crossoverCrossover: The crossover has the purpose of create offsprings during the evolution. After the mating selection the parents are passed to the crossover operator which will dependent on the implementation create a different number of offsprings.
mutationMutation: Some genetic algorithms rely only on the mutation operation. However, it has shown that increases the performance to perform a mutation after creating the offsprings through crossover as well. Usually the mutation operator needs to be initialized with a probability to be executed. Having a high probability of mutation will most of the time increase the diversity in the population.
eliminate_duplicatesbool: The genetic algorithm implementation has a built in feature that eliminates duplicates after merging the parent and the offspring population. If there are duplicates with respect to the current population or in the offsprings itself they are removed and the mating process is repeated to fill up the offsprings until the desired number of unique offsprings is met.
n_offspringsint (default: None): Number of offspring that are created through mating. By default n_offsprings=None which sets the number of offsprings equal to the population size. By setting n_offsprings=1 a, so called, steady-state version of an algorithm can be achieved.