Mixed Variable ProblemΒΆ
In some cases, variables might have different types; some might be real, discrete (choice), binary, or integer-valued. For those cases, different evolutionary operators must be applied to different types of variables. In pymoo this is supported by defining a MixedVariableProblem where the vars values are set. For example, let us consider the following optimization problem:
[1]:
from pymoo.core.problem import ElementwiseProblem
from pymoo.core.variable import Real, Integer, Choice, Binary
class MixedVariableProblem(ElementwiseProblem):
def __init__(self, **kwargs):
vars = {
"b": Binary(),
"x": Choice(options=["nothing", "multiply"]),
"y": Integer(bounds=(0, 2)),
"z": Real(bounds=(0, 5)),
}
super().__init__(vars=vars, n_obj=1, **kwargs)
def _evaluate(self, X, out, *args, **kwargs):
b, x, z, y = X["b"], X["x"], X["z"], X["y"]
f = z + y
if b:
f = 100 * f
if x == "multiply":
f = 10 * f
out["F"] = f
In order to solve such a problem, pymoo offers MixedVariableGA, which defines different operators for each variable type. For more details, please look at the implementation itself.
[2]:
from pymoo.core.mixed import MixedVariableGA
from pymoo.core.variable import Real, Integer
from pymoo.optimize import minimize
problem = MixedVariableProblem()
algorithm = MixedVariableGA(pop_size=10)
res = minimize(problem,
algorithm,
termination=('n_evals', 1000),
seed=1,
verbose=False)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))
Best solution found:
X = {'b': False, 'x': 'nothing', 'y': 0, 'z': 0.0}
F = [0.]
Moreover, for single-objective optimization, the well-known Hyperparameter optimization framework Optuna can be used (pymoo only wraps to their interface here. Congrats on their excellent work!).
[3]:
from pymoo.algorithms.soo.nonconvex.optuna import Optuna
from pymoo.core.variable import Real, Integer
from pymoo.optimize import minimize
problem = MixedVariableProblem()
algorithm = Optuna()
res = minimize(problem,
algorithm,
termination=('n_evals', 300),
seed=1,
verbose=False)
print("Best solution found: \nX = %s\nF = %s" % (res.X, res.F))
Best solution found:
X = {'b': False, 'x': 'nothing', 'y': 0, 'z': 1.2199019154328795e-05}
F = [1.21990192e-05]
Moreover, if you intend to solve a multi-objective optimization problem, you can either instantiate existing algorithms with MixedVariableMating or add a multi-objective survival to MixedVariableGA. The latter can be realized, for instance by:
[4]:
class MultiObjectiveMixedVariableProblem(ElementwiseProblem):
def __init__(self, **kwargs):
vars = {
"b": Binary(),
"x": Choice(options=["nothing", "multiply"]),
"y": Integer(bounds=(-2, 2)),
"z": Real(bounds=(-5, 5)),
}
super().__init__(vars=vars, n_obj=2, n_ieq_constr=0, **kwargs)
def _evaluate(self, X, out, *args, **kwargs):
b, x, z, y = X["b"], X["x"], X["z"], X["y"]
f1 = z ** 2 + y ** 2
f2 = (z+2) ** 2 + (y-1) ** 2
if b:
f2 = 100 * f2
if x == "multiply":
f2 = 10 * f2
out["F"] = [f1, f2]
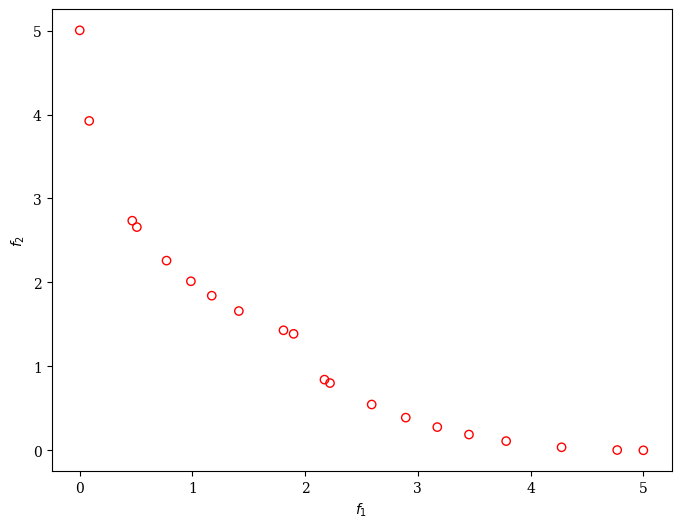
[5]:
from pymoo.visualization.scatter import Scatter
from pymoo.algorithms.moo.nsga2 import RankAndCrowdingSurvival
from pymoo.core.mixed import MixedVariableGA
from pymoo.optimize import minimize
problem = MultiObjectiveMixedVariableProblem()
algorithm = MixedVariableGA(pop_size=20, survival=RankAndCrowdingSurvival())
res = minimize(problem,
algorithm,
('n_gen', 50),
seed=1,
verbose=False)
plot = Scatter()
plot.add(problem.pareto_front(), plot_type="line", color="black", alpha=0.7)
plot.add(res.F, facecolor="none", edgecolor="red")
plot.show()
/var/folders/yq/v2z455rs48b_vb_qzy_22f140000gn/T/ipykernel_27207/3314106399.py:8: DeprecationWarning: RankAndCrowdingSurvival is deprecated and will be removed in version 0.8.*; use RankAndCrowding operator instead, which supports several and custom crowding diversity metrics.
algorithm = MixedVariableGA(pop_size=20, survival=RankAndCrowdingSurvival())
[5]:
<pymoo.visualization.scatter.Scatter at 0x11abf6ed0>
