Rosenbrock¶
The definition ca be found in [54]. It is a non-convex function, introduced by Howard H. Rosenbrock in 1960 and also known as Rosenbrock’s valley or Rosenbrock’s banana function.
Definition
\begin{align} \begin{split} f(x) &=& \sum_{i=1}^{n-1} \bigg[100 (x_{i+1}-x_i^2)^2+(x_i - 1)^2 \bigg] \\ &&-2.048 \leq x_i \leq 2.048 \quad i=1,\ldots,n \end{split} \end{align}
Optimum
\[f(x^*) = 0 \; \text{at} \; x^* = (1,\ldots,1)\]
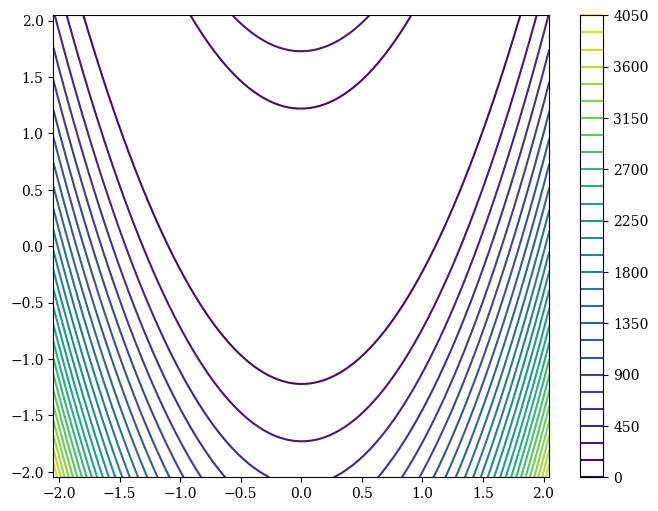
Fitness Landscape
[1]:
import numpy as np
from pymoo.problems import get_problem
from pymoo.visualization.fitness_landscape import FitnessLandscape
problem = get_problem("rosenbrock", n_var=2)
FitnessLandscape(problem, angle=(45, 45), _type="surface").show()
[1]:
<pymoo.visualization.fitness_landscape.FitnessLandscape at 0x10f242060>
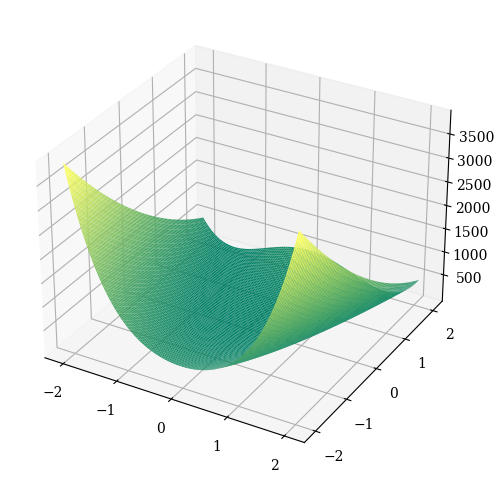
[2]:
FitnessLandscape(problem, _type="contour", colorbar=True).show()
[2]:
<pymoo.visualization.fitness_landscape.FitnessLandscape at 0x11f6849b0>
