R-NSGA-II¶

The implementation details of this algorithm can be found in Reference Point Based Multi-Objective Optimization Using Evolutionary Algorithms [9]. The algorithm follows the general outline of NSGA-II with modified survival selection.

In R-NSGA-II individuals are first selected frontwise. By doing so, there will be the situation where a front needs to be split because not all individuals are allowed to survive. In this splitting front, solutions are selected based on rank.

The rank is calculated as the euclidean distance to each reference point. The solution closest to a reference point is thus assigned a rank of 1. The best rank for each solution is selected as the rank of that solution.

058117851a8a467caad95df083b63dac

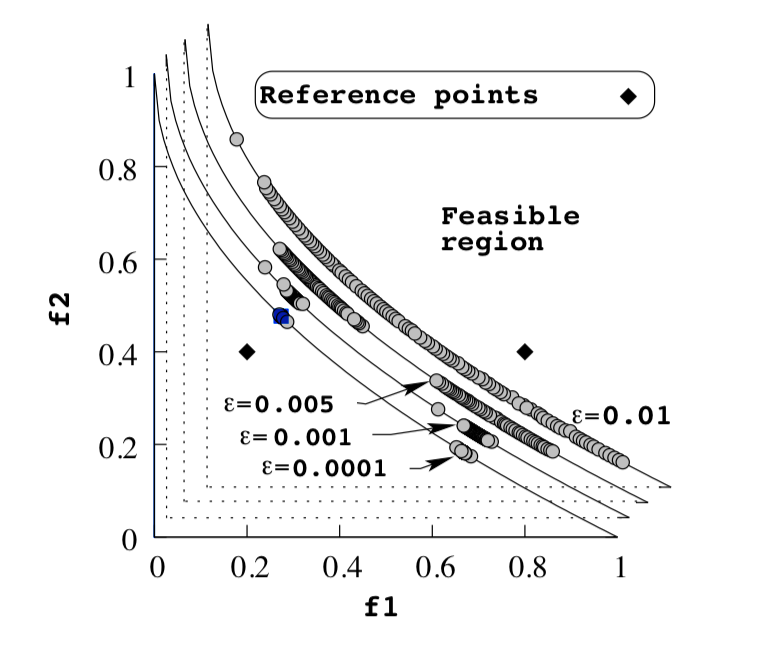
Next, solutions are selected for each reference point frontwise based on rank. After each reference point has selected a solution for survival, all solutions within epsilon distance of surviving solutions are “cleared.” This means that they can not be selected for survival until and unless every front has been processed, and more solutions still need to be selected.

This implies that smaller epsilon values will result in a tighter set of solutions.

Example¶

[1]:

import numpy as np

from pymoo.algorithms.moo.rnsga2 import RNSGA2
from pymoo.problems import get_problem
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter

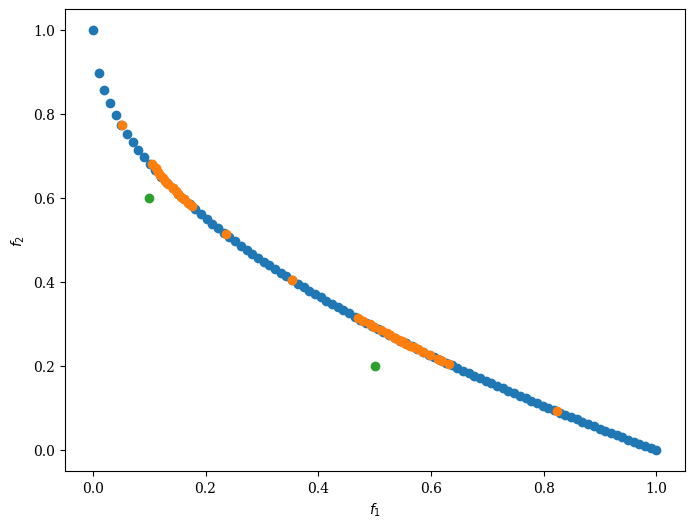
problem = get_problem("zdt1", n_var=30)
pf = problem.pareto_front()

# Define reference points
ref_points = np.array([[0.5, 0.2], [0.1, 0.6]])

# Get Algorithm
algorithm = RNSGA2(
    ref_points=ref_points,
    pop_size=40,
    epsilon=0.01,
    normalization='front',
    extreme_points_as_reference_points=False,
    weights=np.array([0.5, 0.5]))

res = minimize(problem,
               algorithm,
               save_history=True,
               termination=('n_gen', 250),
               seed=1,
               pf=pf,
               disp=False)


Scatter().add(pf, label="pf").add(res.F, label="F").add(ref_points, label="ref_points").show()

[1]:

<pymoo.visualization.scatter.Scatter at 0x126afb6e0>

../../_images/algorithms_moo_rnsga2_7_1.png

API¶

class pymoo.algorithms.moo.rnsga2.RNSGA2(self, ref_points, epsilon=0.001, normalization='front', weights=None, extreme_points_as_reference_points=False, **kwargs)

Parameters

ref_pointsnumpy.array: Reference Points (or also called Aspiration Points) as a numpy.array where each row represents a point and each column a variable (must be equal to the objective dimension of the problem)
epsilonfloat
weightsnp.array
normalization{‘no’, ‘front’, ‘ever’}
extreme_points_as_reference_pointsbool