NSGA-II: Non-dominated Sorting Genetic Algorithm¶

The algorithm is implemented based on [5]. The algorithm follows the general outline of a genetic algorithm with a modified mating and survival selection. In NSGA-II, first, individuals are selected frontwise. By doing so, there will be the situation where a front needs to be split because not all individuals are allowed to survive. In this splitting front, solutions are selected based on crowding distance.

2d05fd2f49f34535bcf297233cdbefcc

The crowding distance is the Manhatten Distance in the objective space. However, the extreme points are desired to be kept every generation and, therefore, get assigned a crowding distance of infinity.

0af83843f77f4331a94990180b881fb9

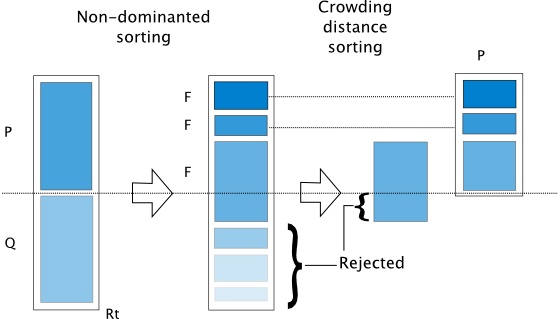
Furthermore, to increase some selection pressure, NSGA-II uses a binary tournament mating selection. Each individual is first compared by rank and then crowding distance. There is also a variant in the original C code where instead of using the rank, the domination criterion between two solutions is used.

Example¶

[1]:

from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.problems import get_problem
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter

problem = get_problem("zdt1")

algorithm = NSGA2(pop_size=100)

res = minimize(problem,
               algorithm,
               ('n_gen', 200),
               seed=1,
               verbose=False)

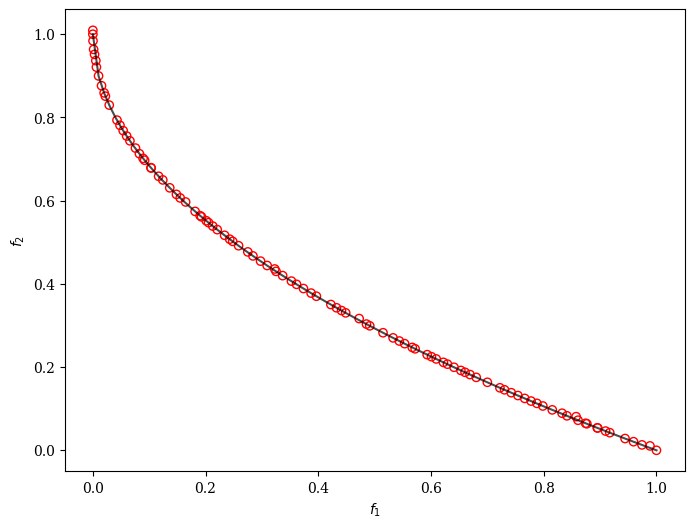
plot = Scatter()
plot.add(problem.pareto_front(), plot_type="line", color="black", alpha=0.7)
plot.add(res.F, facecolor="none", edgecolor="red")
plot.show()

[1]:

<pymoo.visualization.scatter.Scatter at 0x11b307920>

../../_images/algorithms_moo_nsga2_10_1.png

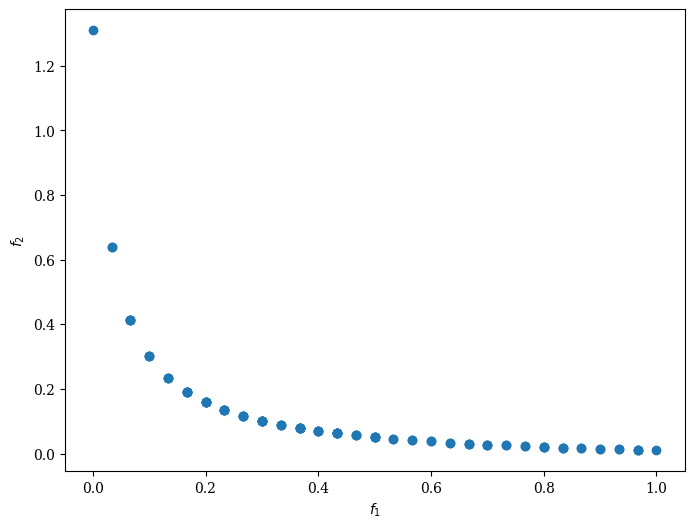
Moreover, we can customize NSGA-II to solve a problem with binary decision variables, for example, ZDT5.

[2]:

from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.problems import get_problem
from pymoo.operators.crossover.pntx import TwoPointCrossover
from pymoo.operators.mutation.bitflip import BitflipMutation
from pymoo.operators.sampling.rnd import BinaryRandomSampling
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter

problem = get_problem("zdt5")

algorithm = NSGA2(pop_size=100,
                  sampling=BinaryRandomSampling(),
                  crossover=TwoPointCrossover(),
                  mutation=BitflipMutation(),
                  eliminate_duplicates=True)

res = minimize(problem,
               algorithm,
               ('n_gen', 500),
               seed=1,
               verbose=False)

Scatter().add(res.F).show()

[2]:

<pymoo.visualization.scatter.Scatter at 0x147a52810>

../../_images/algorithms_moo_nsga2_12_1.png

API¶

class pymoo.algorithms.moo.nsga2.NSGA2(pop_size=100, sampling=<pymoo.operators.sampling.rnd.FloatRandomSampling object>, selection=<pymoo.operators.selection.tournament.TournamentSelection object>, crossover=<pymoo.operators.crossover.sbx.SBX object>, mutation=<pymoo.operators.mutation.pm.PM object>, survival=<pymoo.operators.survival.rank_and_crowding.classes.RankAndCrowding object>, output=<pymoo.util.display.multi.MultiObjectiveOutput object>, **kwargs)