Discrete Variable Problem¶
Mostly, pymoo was made for continuous problems, but of course, other variable types can be used as well. The genetic algorithm is a very modular class, and by modifying the sampling, crossover, and mutation (in some cases also repair), different kinds of variable types can be used (also more complicated ones such as tree, graph, …)
In the following we consider an easy optimization problem where only integer variables are supposed to be used.
[1]:
import numpy as np
from pymoo.algorithms.soo.nonconvex.ga import GA
from pymoo.core.problem import Problem
from pymoo.operators.crossover.sbx import SBX
from pymoo.operators.mutation.pm import PM
from pymoo.operators.repair.rounding import RoundingRepair
from pymoo.operators.sampling.rnd import IntegerRandomSampling
from pymoo.optimize import minimize
class MyProblem(Problem):
def __init__(self):
super().__init__(n_var=2, n_obj=1, n_ieq_constr=1, xl=0, xu=10, vtype=int)
def _evaluate(self, x, out, *args, **kwargs):
out["F"] = - np.min(x * [3, 1], axis=1)
out["G"] = x[:, 0] + x[:, 1] - 10
problem = MyProblem()
method = GA(pop_size=20,
sampling=IntegerRandomSampling(),
crossover=SBX(prob=1.0, eta=3.0, vtype=float, repair=RoundingRepair()),
mutation=PM(prob=1.0, eta=3.0, vtype=float, repair=RoundingRepair()),
eliminate_duplicates=True,
)
res = minimize(problem,
method,
termination=('n_gen', 40),
seed=1,
save_history=True
)
print("Best solution found: %s" % res.X)
print("Function value: %s" % res.F)
print("Constraint violation: %s" % res.CV)
Best solution found: [3 7]
Function value: [-7.]
Constraint violation: [0.]
[2]:
import matplotlib.pyplot as plt
from pymoo.util import plotting
_X = np.row_stack([a.pop.get("X") for a in res.history])
feasible = np.row_stack([a.pop.get("feasible") for a in res.history])[:, 0]
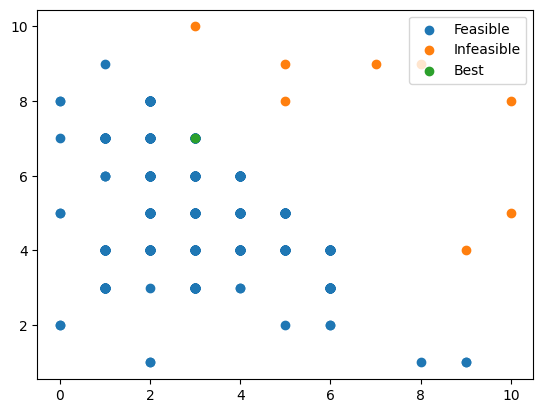
plotting.plot(_X[feasible], _X[np.logical_not(feasible)], res.X[None,:]
, labels=["Feasible", "Infeasible", "Best"])
