Multi-Criteria Decision Making (MCDM)#
The focus of pymoo is on optimization methods itself. However, some basic multi-criteria decision making methods are available:
Compromise Programming#
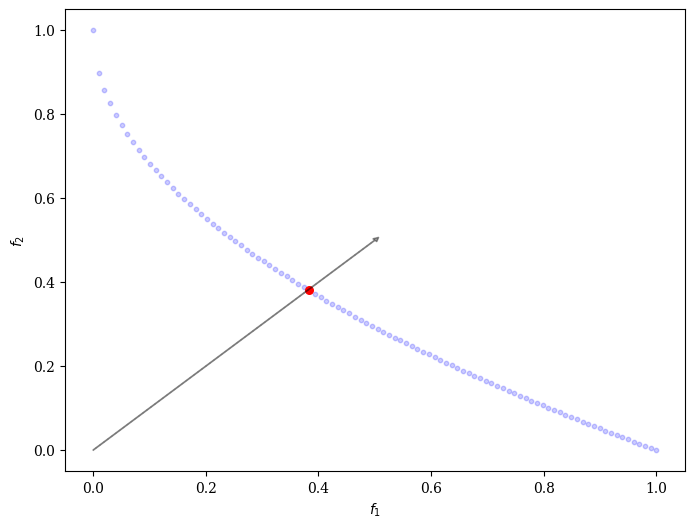
We can use any scalarization method and use it for post-processing. Let us assume our algorithm has converged to the Pareto-front:
[1]:
from pymoo.problems import get_problem
F = get_problem("zdt1").pareto_front()
Then, we initialize weights and our decomposition function:
[2]:
import numpy as np
from pymoo.decomposition.asf import ASF
weights = np.array([0.5, 0.5])
decomp = ASF()
We apply the decomposition and retrieve the best value (here minimum):
[3]:
I = decomp(F, weights).argmin()
print("Best regarding decomposition: Point %s - %s" % (I, F[I]))
Best regarding decomposition: Point 38 - [0.38383838 0.38045308]
Visualize it:
[4]:
import numpy as np
from pymoo.visualization.scatter import Scatter
F = np.array(F)
plot = Scatter()
plot.add(F, color="blue", alpha=0.2, s=10)
plot.add(np.array([F[I]]), color="red", s=30)
plot.do()
plot.apply(lambda ax: ax.arrow(0, 0, *weights, color='black',
head_width=0.01, head_length=0.01, alpha=0.4))
plot.show()
[4]:
<pymoo.visualization.scatter.Scatter at 0x105ce6e90>
Pseudo-Weights#
A simple way to choose a solution out of a solution set in the context of multi-objective optimization is the pseudo-weight vector approach proposed in [1]. Respectively, the pseudo weight \(w_i\) for the i-ith objective function can be calculated by:
\begin{equation} w_i = \frac{(f_i^{max} - f_i {(x)}) \, /\, (f_i^{max} - f_i^{min})}{\sum_{m=1}^M (f_m^{max} - f_m (x)) \, /\, (f_m^{max} - f_m^{min})} \end{equation}
This equation calculates the normalized distance to the worst solution regarding each objective \(i\). Please note that for non-convex Pareto fronts the pseudo weight does not correspond to the result of an optimization using the weighted sum. However, for convex Pareto-fronts the pseudo weights are an indicator of the location in the objective space.
[5]:
from pymoo.mcdm.pseudo_weights import PseudoWeights
from pymoo.util.ref_dirs import get_reference_directions
from pymoo.visualization.petal import Petal
ref_dirs = get_reference_directions("das-dennis", 4, n_partitions=12)
F = get_problem("dtlz1").pareto_front(ref_dirs)
F = np.array(F)
weights = np.array([0.25, 0.25, 0.25, 0.25])
a, pseudo_weights = PseudoWeights(weights).do(F, return_pseudo_weights=True)
weights = np.array([0.4, 0.20, 0.15, 0.25])
b, pseudo_weights = PseudoWeights(weights).do(F, return_pseudo_weights=True)
plot = Petal(bounds=(0, 0.5), reverse=True)
plot.add(F[[a, b]])
plot.show()
Cannot plot a one dimensional array.
Cannot plot a one dimensional array.
Cannot plot a one dimensional array.
Cannot plot a one dimensional array.
Cannot plot a one dimensional array.
Cannot plot a one dimensional array.
Cannot plot a one dimensional array.
Cannot plot a one dimensional array.
Cannot plot a one dimensional array.
Cannot plot a one dimensional array.
[5]:
<pymoo.visualization.petal.Petal at 0x1071621d0>
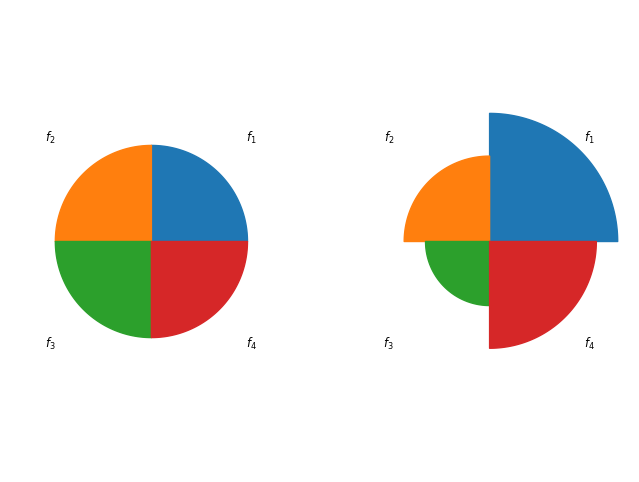
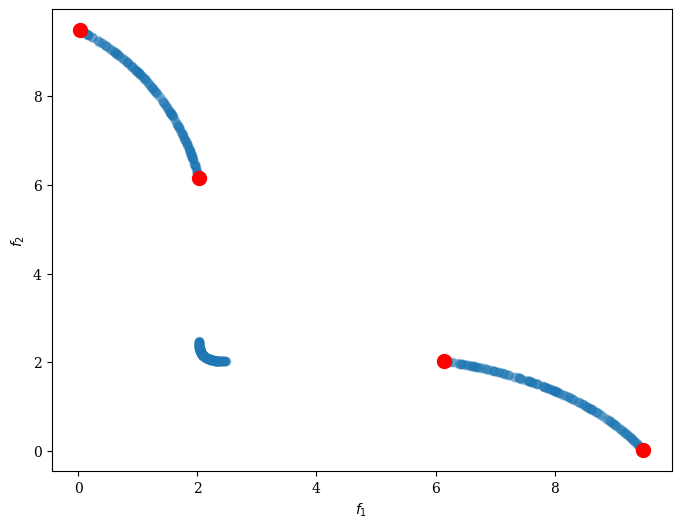
High Trade-off Points#
Furthermore, high trade-off points are usually of interest. We have implemented the trade-off metric proposed in [46]. An example for 2 and 3 dimensional solution is given below:
[6]:
import os
import numpy as np
from pymoo.visualization.scatter import Scatter
from pymoo.mcdm.high_tradeoff import HighTradeoffPoints
pf = np.loadtxt("knee-2d.out")
dm = HighTradeoffPoints()
I = dm(pf)
plot = Scatter()
plot.add(pf, alpha=0.2)
plot.add(pf[I], color="red", s=100)
plot.show()
[6]:
<pymoo.visualization.scatter.Scatter at 0x1074f7b50>
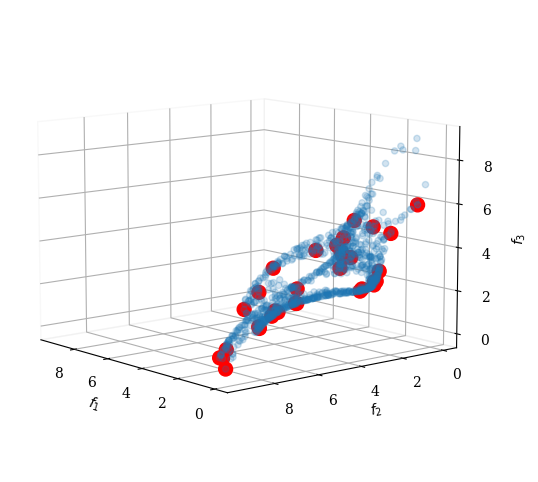
[7]:
pf = np.loadtxt("knee-3d.out")
I = dm(pf)
plot = Scatter(angle=(10, 140))
plot.add(pf, alpha=0.2)
plot.add(pf[I], color="red", s=100)
plot.show()
[7]:
<pymoo.visualization.scatter.Scatter at 0x10758ec50>