PI-NSGA-II: Progressively Interactive NSGA-II

PI-NSGA-II (PINSGA2) is an implementation of PI-EMO-VF [38] for the NSGA-II algorithm. It interactively employs user preferences to guide the multi-objective optimization process using a custom domination operator.

At regular intervals (\(\tau\) generations), the algorithm pauses to select \(\eta\) well-spaced points from the current Pareto front. These points are presented to the decision-maker, who ranks them based on personal preference. The ranking can be either pairwise, where solutions are compared in pairs to establish a relative preference order, or absolute where solutions are ranked from highest to lowest preference. Ranking can either be made by a human decision maker via the command line, or automatically with a programmed automatic decision maker.

The user-provided rankings are then used to fit a value function that models the decision maker’s preferences. This value function modifies the domination of points for the next \(\tau\) generations, and then the process is repeated.

Example

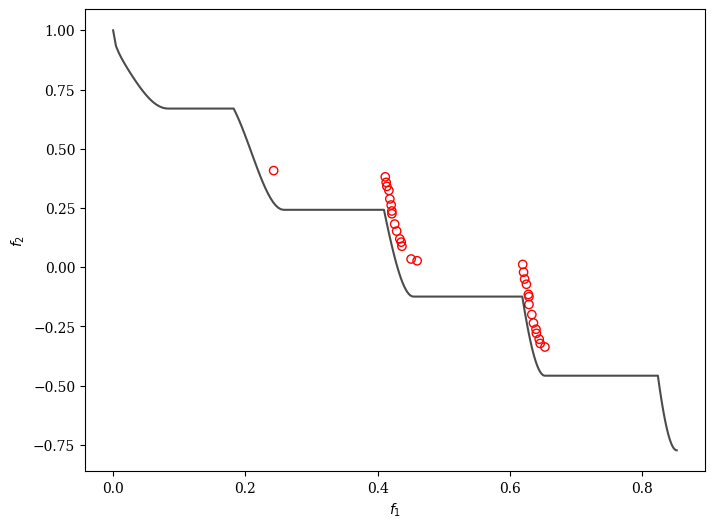
This is a simple example with a custom automatedDM. This example uses ZDT3, since its disconnected Pareto-optimal front illustrates how the algorithm guides the optimization through the objective space. The decision maker is set to rank four points (\(\eta\)) every ten generations (\(\tau\)) based on their distance from the center of the second region of the solution. In this case imagine the decision maker only wants one or more solutions in this area of the search space, and the other solutions are undesirable.

from pymoo.algorithms.moo.pinsga2 import PINSGA2, AutomatedDM
from pymoo.problems import get_problem
from pymoo.optimize import minimize
import numpy as np
from pymoo.visualization.scatter import Scatter

class simpleDM( AutomatedDM ):

    def makeDecision(self, F):
        # Euclidean distance from center of region # 2
        distances = np.sqrt( ( F[:, 0] - 0.21999557 )**2 + ( 0.40167775 - F[:, 1] )**2 )

        if distances[0] < distances[1]:
            out = 'a'
        elif distances[1] < distances[0]:
            out = 'b'
        else:
            out = 'c'

        return out

simple_dm = simpleDM()

problem = get_problem("zdt3")

algorithm = PINSGA2(pop_size=30,
                    tau=10,
                    eta=4,
                    opt_method="trust-constr",
                    vf_type="poly",
                    ranking_type="pairwise",
                    automated_dm=simple_dm)

res = minimize(problem,
               algorithm,
               ('n_gen', 100),
               seed=1,
               verbose=False)

plot = Scatter()
plot.add(problem.pareto_front(), plot_type="line", color="black", alpha=0.7)
plot.add(res.F, facecolor="none", edgecolor="red")
plot.show()

/Users/blankjul/anaconda3/envs/pymoo-doc/lib/python3.10/site-packages/scipy/optimize/_differentiable_functions.py:552: UserWarning: delta_grad == 0.0. Check if the approximated function is linear. If the function is linear better results can be obtained by defining the Hessian as zero instead of using quasi-Newton approximations.
  self.H.update(delta_x, delta_g)

<pymoo.visualization.scatter.Scatter at 0x109b37700>

Parameters

Name	Description	Parameter	Possible values
τ (tau)	Number of generations between each stakeholder prompt	tau	1 < τ (default: 10)
η (eta)	Number of points for the decision maker to rank each τ generations	eta	2 < η (default: 4)
Optimization method	The optimization method used to fit the value function	opt_method	trust-constr (default), SLSQP, ES, GA
Value function type	The mathematical format of your value function	vf_type	poly (default): polynomial representation, linear: linear representation
Ranking method	The method of eliciting preference from the stakeholder	ranking_method	pairwise (default): compare two solutions at a time, absolute: complete ranking
Automated ranking	Whether to use automated decision maker instead of human	automated_dm	A class that implements the AutomatedDM class

API

class pymoo.algorithms.moo.pinsga2.PINSGA2(pop_size=100, sampling=<pymoo.operators.sampling.rnd.FloatRandomSampling object>, selection=<pymoo.operators.selection.tournament.TournamentSelection object>, crossover=<pymoo.operators.crossover.sbx.SBX object>, mutation=<pymoo.operators.mutation.pm.PM object>, output=<pymoo.util.display.multi.MultiObjectiveOutput object>, tau=10, eta=4, opt_method='trust-constr', vf_type='poly', eps_max=1000, ranking_type='pairwise', presi_signs=None, automated_dm=None, verbose=False, **kwargs)